大 $O$ 符号与渐近分析

在阅读本章时，请先抛开算法中关于 大$O$ 的一些定义，先从数学的角度来理解 大$O$。另外这部分是纯数学理论。大部分内容来自《离散数学及其应用》的第三章。

阅读本部分内容需要有函数、极限相关的数学知识。

函数的渐近增长与大 $O$ 符号

当人们讨论用于执行特定任务的快速或高效的算法时，意味着一种算法要快或高效吗？几秒钟、几分钟并不是一个实际的测量值。因为计算机硬件差异很大，那么这个测量值的结果也会有很大的差异。

我们不能用算法的运行时间（几秒钟、几分钟）来衡量两个算法的效率，要创建一个统一的度量标准，计算机科学家和数学家们设计了测试程序的渐近复杂性（Asymptotic Complexity）的概念和符号大 $O$ 用于描述算法运行的效率。

使用 大$O$ 符号(Big-$O$ notation) 有一个好处，就是可以估算一个函数的增长而不用担心常数因子或低阶项。这意味着使用大 $O$ 符号不用担心实现算法所用的硬件和软件。另外，使用大 $O$ 符号时我们可以假设算法中使用的不同操作都花费相等的时间，这大大简化了分析。

Big $O$

a function $f(x)$ runs on the order $g(x)$ if there exists some $x$ value ($x_0$), and some constant $C$, for which $f(x)$ is less than or equal to that constant times $g(x)$ for all $x$ greater than $x_0$. We say that $f(x)$ is $O(g(x))$.(这句是补充的)

上面定义的数学符号描述。

$$\begin{array}{c} f(x) \in g(x) \\ \\ \exist x_0, \exist C, \forall{x}(x > x_0), \quad f(x) \le C \cdot g(x) \end{array}$$

提示

关于这里的符号 “$\in$” 后文中有解释。

《离散数学及其应用》中的定义可能更好理解一些。

大$O$符号

令 $f$ 和 $g$ 为从整数集或实数集到实数集的函数。如果存在常数 $C$ 和 $k$ 使得只要 $x > k$ 时就有 $$|f(x)| \le C|g(x)|$$

我们就说 $f(x)$ 是 $O(g(x))$ 的。[这个可以读作“$f(x)$ 是大 $Og(x)$ 的”]

要证明$f(x)$ 是 $O(g(x))$ 的，我们需要找出一对常数 $C$ 和 $k$，即凭证，使得只要当 $x>k$ 时就有 $|f(x)| \le C|g(x)|$。

利用大 $O$ 记号的定义 求一对凭证的一种有用方法时先选择 $k$ 的值使得当 $x > k$ 时容易估算 $|f(x)|$ 的大小，再看看能否用这个估算找出 $C$ 的值使得对于 $x > k$ 时有 $|f(x)| < C|g(x)|$

提示

如果按照定义，考虑$f(x) = 10x^2 + 10x$ 而 $g(x) = x^3$，令$C = 10, k = 2$，则有

$$f(x) = 10x^2 + 10x < C\cdot g(x) = 10x^3,(x > 2)$$

在上例中，我们找出了一组 $C,k$ 使得 $f(x) \le C\cdot g(x)$ 那我们是不是可以说 $f(x)$ 是 $O(g(x))$ 的呢？

答案是：可以

这里可能与会我们之前看到的关于大$O$的说法不一样，但是大$O$本来的定义就是为了描述函数的渐近增长。也即当 $x > k$时函数$C\cdot g(x)$的增长速度要快于 $f(x)$

例题： 证明 $f(x) = x^2 + 2x + 1$ 是 $O(x^2)$的。

Proof

解：观察到当 $x > 1$ 时可以容易估算 $f(x)$ 的大小，因为当 $x > 1$ 时 $x < x^2$ 且 $1 < x^2$。所以当 $x > 1$ 时就有

$$0 \le x^2 + 2x +1 \le x^2 + 2x^2 + x^2 = 4x^2$$

如下图所示。因此，可以取 $C = 4$ 和 $k = 1$ 作为凭证以证明 $f(x)$ 是 $O(x^2)$。即只要当 $x > 1$ 时就有 $f(x) = x^2 + 2x +1 < 4x^2$

评注

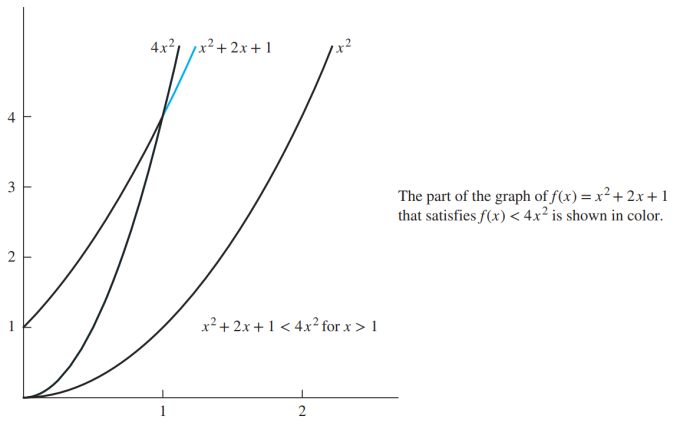
$f(x)$ 是 $O(g(x))$ 的事实有时写作 $f(x) = O(g(x))$。不过这一写法中的等号并不代表真正的相等，而是告诉我们对于这些函数定义域中足够的的数而言，函数 $f$ 和 $g$ 的值之间有不等式成立。然而 $f(x) \in O(g(x))$ 这样的写法也是可接受的，因为 $O(g(x))$ 可以表示那些是 $O(g(x))$ 函数的集合。

当 $f(x)$ 是 $O(g(x))$ 的，并且对于足够大的 $x$ 有函数 $h(x)$ 的绝对值大于 $g(x)$，则有 $f(x)$ 是 $O(h(x))$ 的。换言之，在 $f(x)$ 是 $O(g(x))$ 的这一关系中的函数 $g(x)$ 可以替换为具有更大绝对值的函数。如果

$$|f(x)| \le C|g(x)| \qquad \text{如果} \: x > k$$

并且如果对所有 $x > k$ 有 $|h(x)| > |g(x)|$，那么

$$|f(x)| \le C|h(x)| \qquad \text{如果} \: x > k$$

故，$f(x)$ 是 $O(h(x))$ 的。

一些重要函数的大$O$估算

定理1

令 $f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + \dots + a_{1}x + a_{0}$，其中 $a_0,a_1, \dots, a_{n-1}, a_n$ 为实数。那么 $f(x)$是$O(x^n)$ 的。

《离散数学及其应用》第8版，3.2.3，P187

Proof

用三角不等式，如果 $x > 1$，就有

$$\begin{array}{rl} |f(x)| &= |a_{n}x^{n} + a_{n-1}x^{n-1} + \dots + a_{1}x + a_{0}| \\ \\ & \le |a_{n}|x^{n} + |a_{n-1}|x^{n-1} + \dots + |a_{1}|x + |a_{0}| \\ \\ & = x^n(|a_{n}| + |a_{n-1}|/x + \dots + |a_{1}|x^{n -1} + |a_{0}|/x^n) \\ \\ & \le x^n(|a_{n}| + |a_{n-1}| + \dots + |a_{1}| + |a_{0}|) \end{array}$$

这说明只要当 $x>1$ 时就有

$$|f(x)| \le Cx^n$$

其中 $C = |a_{n}| + |a_{n-1}| + \dots + |a_{1}| + |a_{0}|$

提示

三角不等式 $|a + b| \le |a| + |b|$

函数组合的增长

许多算法都由两个或多个独立的子过程组成。计算机使用这样的算法来求解一定输入规模的问题时所需要的步数就是这些过程所使用的步数之和。要用大$O$估算所需要的步数，就需要找出每个子过程所用步数的大$O$估算，然后再把这些估算组合起来。

假定 $f_{1}(x)$ 是 $O(g_{1}(x))$ 的，$f_{2}(x)$ 是 $O(g_{2}(x))$ 的，两个函数之和与之积会有怎样的估算。

由大$O$的定义可知，存在常数 $C_1,\:C_2,\:k_1,\:k_2$ 使得当 $x < k_1$ 时有

$$|f_1(x)| \le C_1|g_1(x)|$$

而当 $x > k_2$ 时有

$$|f_2(x)| \le C_2|g_2(x)|$$

要估算 $f_{1}(x)$ 与 $f_{2}(x)$ 之和，请注意

$$\begin{array}{rcl} |(f_1 + f_2)(x)| &=& |f_1(x) + f_2(x)| \\ & \le & |f_1(x)| + |f_2(x)| \end{array}$$

当 $x$ 同时大于 $k_1$ 和 $k_2$ 时，从 $|f_1(x)|$ 和 $|f_2(x)|$的不等式可得：

$$\begin{array}{rcl} |f_1(x)| + |f_2(x)| & \le & C_1|g_1(x)| + C_2|g_2(x)| \\ & \le & C_1|g(x)| + C_2|g(x)| \\ & = & (C_1 + C_2)|g(x)| \\ & = & C|g(x)| \\ \end{array}$$

其中 $C = C_1 + C_2$ 且 $g(x) = (\max(\:| g_1(x) |,\:|g_2(x)|\:))$。由此我们可以得出定理2

定理2

假定 $f_{1}(x)$ 是 $O(g_{1}(x))$ 的，$f_{2}(x)$ 是 $O(g_{2}(x))$ 的，那么 $(f_1 + f_2)(x)$ 是 $O(g(x))$ 的，其中对所有 $x$ 有 $g(x) = (\max(\:| g_1(x) |,\:|g_2(x)|\:))$。

由定理2可以得出如下推论。

推论1

假定$f_1(x)$ 和 $f_2(x)$ 都是 $O(g(x))$ 的，那么 $(f_1 + f_2)(x)$ 也是 $O(g(x))$ 的

用类似的方法可以推导出 $f_{1}(x)$ 和 $f_{2}(x)$ 乘积的大$O$估算。当 $x > \max(k_1,k_2)$时，可得出

$$\begin{array}{rcl} |(f_1f_2)(x)| & = & |f_1(x)||f_2(x)| \\ & \le & C_1|g_1(x)| C_2|g_2(x)| \\ & \le & C_1C_2|(g_1g_2)(x)| \\ & \le & C|(g_1g_2)(x)| \end{array}$$

其中 $C = C_1C_2$。从这一不等式可知 $f_1(x)f_2(x)$ 是 $O(g_1g_2)$ 的，因为存在常数 $C$ 和 $k$，即 $C = C_1C_2$ 和 $k = \max(k_1,K_2)$，使得只要 $x > k$ 时就有 $|(f_1f_2(x))| \le C|g_1(x)g_2(x)|$。这一结果可表述为定理3.

定理3

假定 $f_{1}(x)$ 是 $O(g_{1}(x))$ 的，$f_{2}(x)$ 是 $O(g_{2}(x))$ 的，那么 $(f_1f_2)(x)$ 是 $O(g_1(x)g_2(x))$ 的。

大 $Ω$ 与大 $Θ$ 符号

大$O$符号广泛用于描述函数的增长，但它也有局限性。特别是，当$f(x)$是$O(g(x))$是，我们只有用$g(x)$来估算对于大$x$值的$f(x)$大小的一个上限。而不能提供对大$x$值的$f(x)$之大小的一个下限。

• 我们使用大$\mathbf{Ω}$ 符号，来估算对于大$x$值的$f(x)$之大小的一个下限。
• 我们使用大$\mathbf{Θ}$ 符号，给出函数$f(x)$的相对于参照函数$g(x)$的上限和下限。

大 $Ω$ 与大 $Θ$ 符号都是由高德纳在 1970 年引入的。他引入这两个符号的动机是纠正人们需要用到函数的上限和下限时对大 $O$ 符号的误用。

大 $\mathbf{Ω}$

令 $f$ 和 $g$ 为从整数集合或实数集合到实数集合的函数。如果存在正常数 $C$ 和 $k$ 使得当 $x > k$ 时有 $$|f(x)| \ge C|g(x)|$$

我们就说 $f(x)$ 是 $\Omega(g(x))$ 的。[这个可以读作“$f(x)$ 是大 $\Omega g(x)$ 的”]

注意定义中的公式，这里是 $\ge$，而大$O$中是$\le$。大 $\Omega$ 与大$O$正好相反。

大 $\mathbf{Θ}$

令$f$和$g$为从整数集合或实数集合到实数集合的函数。如果$f(x)$是$O(g(x))$的，且$f(x)$是$\Omega(g(x))$的，我们就说$f(x)$是$\varTheta(g(x))$的，当$f(x)$是$\varTheta(g(x))$的，我们说$f(x)$是大西塔（$\varTheta$）$g(x)$的，即$f(x)$是$g(x)$阶的，或$f(x)$和$g(x)$是同阶的。

当$f(x)$是$\varTheta(g(x))$的，同样也会有$g(x)$是$\varTheta(f(x))$的，注意 $f(x)$是$\varTheta(g(x))$的，当且仅当$g(x)$是$\varTheta(f(x))$的。

$f(x)$是$\varTheta(g(x))$的，当且仅当存在实数$C_1$和$C_2$以及一个正实数 $k$ 使得当 $x > k$ 时有

$$C_1|g(x)| \le |f(x)| \le C_2|g(x)|$$

常量$C_1$和$C_2$以及$k$的存在分别告诉我们 $f(x)$是$\Omega(g(x))$的和$f(x)$是$O(g(x))$的。

定理4

令$f(x) = a_{n}x^n + a_{n-1}x^{n-1} + \dots + a_{1}x + a_0$，其中 $a_0, a_1, \dots , a_n$ 为实数且 $a_n \ne 0$。则 $f(x)$ 是 $x^n$ 阶的。

注意不要将大$O$符号，和大$\varTheta$符号混用。近来的趋势是当需要一个函数大小的上界和下界时就采用大$\varTheta$符号。

小 $o$ 与小 $ω$

由 $O$ 记号提供的渐近上界可能是也可能不是渐近紧确的。界 $x^2 =O(x^2)$ 是渐近紧确的，但是界 $x=O(x^2)$ 却不是。我们使用 $o$ 记号来表示一个非渐近紧确的上界。

小 $o$

令 $f$ 和 $g$ 为从整数集合或实数集合到实数集合的函数。对于任意常量 $C > 0$ ，存在常量 $k > 0$，使得对所有 $x \ge k$ 时有 $$0 \le f(x) \le C \cdot g(x)$$

我们说 $f(x)$ 是 $o(g(x))$ 的。

例如，$2x = o(x^2)$，但是 $2x^2 \ne o(x^2)$

在 $o$ 记号中，当 $x \to \infty$ 时，函数 $f(x)$ 相对于 $g(x)$ 来说变得微不足道了。即

$$\lim_{x \to \infty} \frac{f(x)}{g(x)} = 0$$

有些学者使用这个极限作为 $o$ 记号的定义，但在这里还需要限定函数是渐近非负的。

$w$ 记号与 $\Omega$ 记号的关系类似千 $o$ 记号与 $O$ 记号的关系。我们使用 $w$ 记号来表示一个非渐近紧确的下界

小 $w$

令 $f$ 和 $g$ 为从整数集合或实数集合到实数集合的函数。对于任意常量 $C > 0$ ，存在常量 $k > 0$，使得对所有 $x \ge k$ 时有 $$0 \le C \cdot g(x) \le f(x)$$

我们说 $f(x)$ 是 $w(g(x))$ 的。

他的另一种定义方式是：

$$f(x) \in w(g(x)) \quad \text{当且仅当} \quad g(x) \in o(f(x))$$

关系 $f(x) = w(g(x))$ 蕴含着

$$\lim_{x \to \infty} \frac{f(x)}{g(x)} = \infty$$

也就是说，如果这个极限存在，那么当 $x$ 趋于无穷时， $f(x)$ 相对于 $g(x)$ 来说变得任意大了。

渐近等价

这里补充一部分渐近理论。

考虑一个函数 $f(x)$，我们需要了解当 $x$ 变得非常大的时候 $f(x)$ 的性质。令 $f(x) = x^2 + 3x$，在 $x$ 特别大的时候，第二项 $3x$ 比起第一项 $x^2$ 要小很多。于是对于这个函数有如下断言：

$f(x)$ 在 $x \to \infty$ 的情况下与 $x^2$ 渐近等价，记作 $f(x) ~ x^2$

正式定义

给定关于自然数 $x$ 的复函数 $f$ 和 $g$，命题 $f(x) \sim g(x)(x \to \infty)$ 表明 $$f(x) = g(x) + o(g(x)) (x \to \infty)$$

这说明，对于正常数 $\epsilon$ ，存在常量 $N$，使得对于所有的 $x \ge N$ 有 $$|f(x) - g(x)| \le \epsilon|g(x)|$$

提示

这里的 $o(g(x))$ 表示比 $g(x)$ 低阶的函数。令 $z(x) = o(g(x))$，则$\displaystyle\lim_{x \to \infty}\frac{z(x)}{g(x)} = 0$，或者直接写为：$\displaystyle\lim_{x \to \infty}\frac{o(g(x))}{g(x)} = 0$，其中 $g(x) \ne 0$

当 $g(x)$不是$0$或趋于无穷大时，该命题可等价记作 $\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)} = 1$，也即当$\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)} = 1$时$f(x) \sim g(x)$

关于上面定义的解释

如：$f(x) = x^2 + 2x +1$ ， $g(x) =x^2$，证明 $f(x) \sim g(x)$

若要证明 $f(x) \sim g(x)$，可证明 $\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)} = 1$

证明如下：

$$\begin{array}{rl} \displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)} &= \displaystyle\lim_{x \to \infty}\displaystyle\frac{x^2 + 2x +1}{x^2} \\ \\ & = \displaystyle\lim_{x \to \infty}(1 + \displaystyle\frac{2x}{x^2} +\displaystyle\frac{1}{x^2}) \\ \\ & = 1 + 0 + 0 = 1 \end{array}$$

因此 $f(x) \sim g(x)$

函数的阶

① 若 $\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)} = 0$ ，则记 $f(x) = o(g(x))$ $(x \to \infty)$，且称 $f(x)$ 比 $g(x)$ 低阶。

② 而对于大$O$可以表述为，若 $\displaystyle\frac{f(x)}{g(x)}$有限，则记为 $f(x) = O(g(x))$ $(x \to \infty)$，称$f$的阶不超过$g$。

回顾一下大$O$的定义，可以通过定义简单推导下

$$\begin{array}{c} |f(x)| \le C|g(x)| \\ \to \displaystyle\frac{|f(x)|}{|g(x)|} \le C \end{array}$$

这里的$C$ 是一个常数，因此与上面的表述是等价的。

③ 若$\displaystyle\lim_{x \to \infty}\frac{f(x)}{g(x)} = k$， $k$ 是一个常数，则记为 $f(x) = \varTheta(g(x))$ $(x \to \infty)$ ，且称 $f(x)$ 比 $g(x)$ 同阶。

渐近比较的一些性质

实数的许多关系性质也适用于渐近比较。下面假定 $f(x)$ 和 $g(x)$ 渐近为正。

传递性

$$\begin{array}{lcl} f(x) = \varTheta(g(x)) \land g(x) = \varTheta(h(x)) & \to & f(x) = \varTheta(h(x)) \\ f(x) = O(g(x)) \land g(x) = O(h(x)) & \to & f(x) = O(h(x)) \\ f(x) = \Omega(g(x)) \land g(x) = \Omega(h(x)) & \to & f(x) = \Omega(h(x)) \\ f(x) = o(g(x)) \land g(x) = o(h(x)) & \to & f(x) = o(h(x)) \\ f(x) = w(g(x)) \land g(x) = w(h(x)) & \to & f(x) = w(h(x)) \\ \end{array}$$

自反性

$$\begin{array}{lcl} f(x) & = & \varTheta(f(x)) \\ f(x) & = & O(f(x)) \\ f(x) & = & \Omega(f(x)) \end{array}$$

对称性

$$f(x) = \varTheta(g(x)) \iff g(x) = \varTheta(f(x))$$

转置对称性

$$\begin{array}{lcl} f(x) = O(g(x)) & \iff & g(x) = \Omega(f(x)) \\ f(x) = o(g(x)) & \iff & g(x) = w(f(x)) \end{array}$$

三分性

对任意两个实数 $a$ 和 $b$，下列三种情况恰有一种必须成立：$a<b,a=b,$ 或 $a>b$

虽然任意两个实数都可以进行比较，但是不是所有函数都可渐近比较。也就是说对于两个函数 $f(x)$ 和 $g(x)$，也许 $f(x) = O(g(x))$ 和 $f(x) = \Omega(g(x))$ 都不成立。

大$O$ 还是 大$Θ$

在实际使用过程中，大家更倾向于使用大$O$，而非大$\varTheta$。

关于这个问题，必须要做一下说明。

如果 $f(x)$ 是 $\varTheta(g(x))$ 的，那么它一定是 $O(g(x))$的。 但是反过来并不成立。

来看个例子：$f(x) = 3x^2 + 2x +3$ 。

• 我们可以说 $f(x)$ 是 $O(x^2)$ 的，或说 $f(x)$ 是 $\varTheta(x^2)$的
• 我们可以说 $f(x)$ 是 $O(x^3)$ 的，而不能说 $f(x)$ 是 $\varTheta(x^3)$的。

Note

可以通过定义证明以上结论是正确的，证明过程此处忽略。

这里要强调的是，我们用大$O$来描述算法的运行效率是没有任何问题的。

关于大家习惯于用大$O$而不用$\varTheta$，还有几点原因需要强调下：

• 大$O$符号提供了算法的上界，这对于算法分析中的保守估计非常有用。了解算法在最坏情况下的表现能够帮助开发者做出更可靠的系统设计和性能预估。而且使用起来相对简单。它只需要确定一个上界，不需要找到一个紧确界。对于许多算法分析和讨论来说，了解一个算法的上界通常已经足够。
• 计算机科学和软件工程领域的大量文献和教材中都使用大 $O$ 符号，形成了一个惯例和标准。这种惯例的形成使得大 $O$ 符号成为了默认选择。
• 在理论分析中，大 $\varTheta$ 符号提供了更加精确的信息，因为它表示了算法复杂度的上界和下界。但是，在很多实际应用场景中，特别是当算法分析的重点在于理解其基本性能而非严格的数学证明时，大 $O$ 符号已经足够。

而在《离散数学及其应用》中有这样一句话。

近来的趋势是当需要一个函数大小的上界和下界时就采用大 $\varTheta$ 符号。

因此在后续的文章中我们一般会采用大$O$来描述算法的运行效率，除非需要涉及到严格的数学证明，否则不使用大 $\varTheta$ 符号

总结

当我们分析一个算法的复杂度的时候其实用的是大$\varTheta$理论，当然也不能说大$O$不对，因为大$O$其实是包含大$\varTheta$。只是大$O$没有定义下界，而我们分析一个算法的复杂度的时候，最好的方式是使用大$\varTheta$ 理论来确定 $g(x)$。

令$f(x)=2x^2 + 3x$，令$g(x) = x^2$

当 $C = 3, x > 4$时， 有 $f(x) \le C\cdot g(x)$ 因此 $f(x)$ 是 $O(x^2)$的。
当 $C = 2, x > 0$时， 有 $f(x) \ge C\cdot g(x)$ 因此 $f(x)$ 是 $\Omega(x^2)$的。

因此$f(x)$ 是$\varTheta(g(x))$的。我们就可以说这个算法的复杂度是$O(x^2)$

当然对于$f(x)$，当$g(x)=x^3$时， $f(x)$ 也是 $O(g(x))$ 的，但是我们不能说这个算法的运行时间是$O(x^3)$。

使用渐近等价理论也是可以的，但是我们在说一个算法复杂度的时候常常会忽略常数部分。如：令$f(x)=2x^2 + 3x$，当 $x \to \infty$ 时，$f(x) \sim 2x^2$，而我们常用$O(x^2)$来表达算法的运行效率，而不用$O(2x^2)$

参考资料

• Kenneth H. Rosen. 《离散数学及其应用（原书第8版）》. 机械工业出版社. 2019: P183-P192
• Mark Allen Weiss. 《数据结构与算法分析（Java语言描述符）》. 机械工业出版社. 2008: P22-P42
• Thomas H. Carmen;Charles E. Leiserson等. 《算法导论（原书第三版）》. 机械工业出版社. 2013: P25-P30. ISBN 978-7-111-40701-0
• 维基百科. 渐近分析
• 知乎. 渐近分析：大$O$记号、小$o$记号与“$~$”记号
• 腾讯云. 彤哥. $O$、$Θ$、$Ω$、$o$、$ω$，别再傻傻分不清了！