链表

链表是一种常见的基础数据结构，是一种线性表。链表中的每个元素都存储有下个元素的指针，通过首尾相接的方式将所有元素有序的串在一起。链表并不要求所有元素在内存中的位置是相邻的，所有元素都可以分散地存储在内存中。

链表的分类

注意

注意：插入元素的时间复杂度是 $O(1)$ ，这是因为在计算这个时间复杂度的时候并没有计算查找元素的时间。如向 $P_k$ 后插入一个元素 $Q$ 。这时候只需要将 $P_k$ 的下一个节点的指针指向 $Q$ ， $Q$ 的下一个节点的指针指向 $P_{k+1}$ 。

\begin{array}{l} \boxed{P_k} \to \boxed{P_{k+1}} \\ \\ \boxed{P_k} \to \boxed{Q} \to \boxed{P_{k+1}} \end{array}

这个两个操作的时间复杂度都是常数级的。因此时间复杂度是 $O(1)$ 。但是请注意找到 $P_k$ 这个元素的时间复杂度可是 $O(n)$ 。

在已获取到 $P_k$ 的情况下，向 $P_k$ 后插入一个元素的时间复杂度是 $O(1)$ 。在未知 $P_k$ 的情况下，向 $P_k$ 后插入一个元素的时间复杂度是 $O(n)$ 。

在链表中为了表示每个数据 $a_i$ 与 $a_{i+1}$ 之间的逻辑关系，对于数据元素 $a_i$ 来说，除了要存储其本身的信息外，还需要存储一个指向 $a_{i+1}$ 的指针。

存储数据元素信息的域称为数据域，存储直接后继指针或直接前驱指针的域称为指针域。这两部分信息组成数据元素 $a_i$ 的存储映像，称为节点(Node)，有的地方也叫结点。后文中我们统一用节点。

链表结构

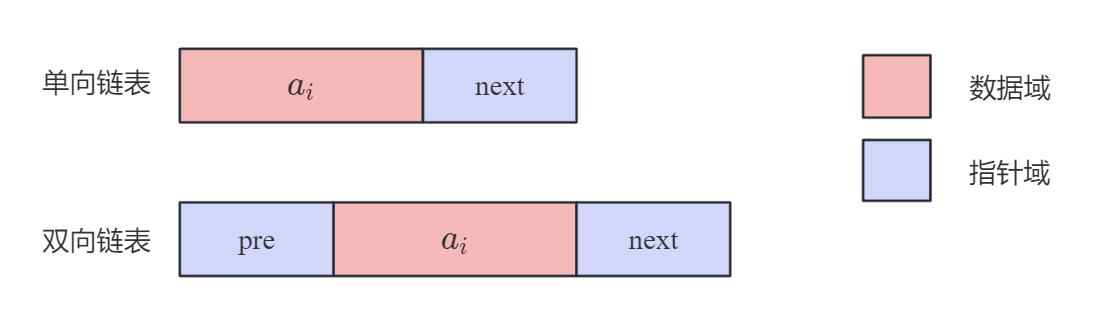
头节点（Head Node）：头节点是链表的起始节点，它没有前驱节点。在单向链表中，头节点通常用于表示链表的开始。

尾节点（Tail Node）：尾节点是链表的最后一个节点，它没有后继节点。在单向链表中，尾节点通常用于表示链表的结束。

前驱节点（Previous Node）：前驱节点是指链表中当前节点的前一个节点。在单向链表中，每个节点只有一个指向下一个节点的指针，因此没有前驱节点的概念。

后继节点（Next Node）：后继节点是指链表中当前节点的下一个节点。在单向链表中，每个节点只有一个指向下一个节点的指针，因此后继节点是指向当前节点的下一个节点。

链表长度（Linked List Length）：链表长度是指链表中节点的数量。在单向链表中，可以通过遍历链表来计算链表的长度。

优点：

缺点：

提示

关于链表的优缺点可以在后续的文章中体会。