单向链表
单向链表的特点是链表的链接方向是单向的,对链表的访问要通过从头部开始,依序往下读取。
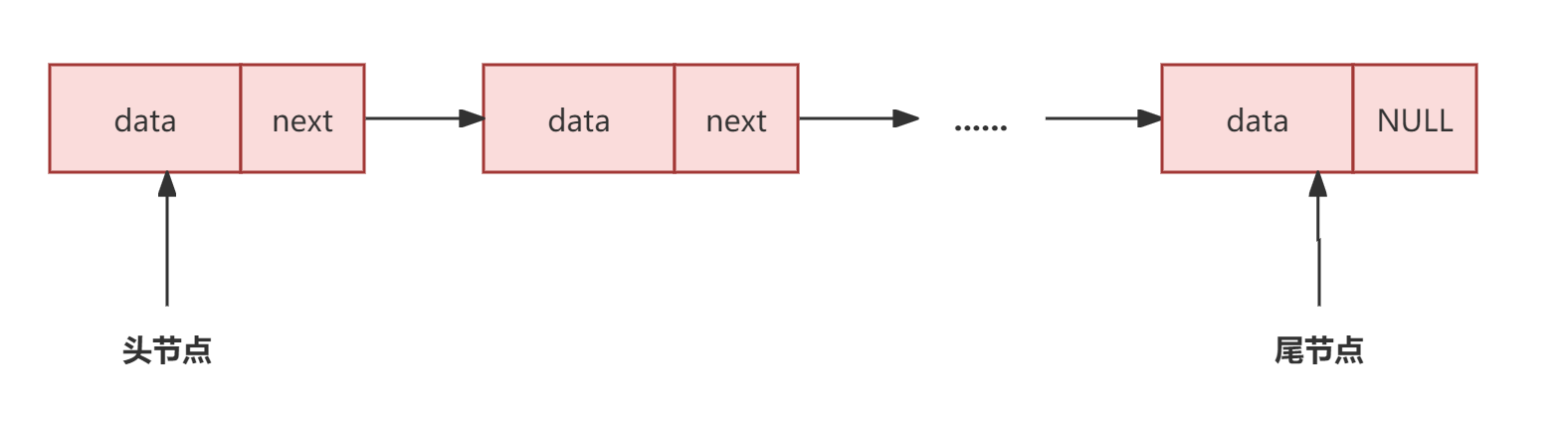
节点结构
一个单向链表的节点包含两个部分,数据和指向下一个节点的指针。单向链表只可以从头开始遍历。
@NoArgsConstructor
@Data
public class Node<T> {
/**
* 数据
*/
private T data; 1
/**
* 指向下一个节点的指针
*/
private Node<T> next; 2
public Node(T data) {
this.data = data;
}
}
数据域:存放元素自身的数据信息。
指针域:指向节点的后继。
利用单链表可以解决数组需要大量连续存储单元的缺点,以及数组无法动态扩容的缺点。由于单链表节点离散的存储在内存中,所以无法实现对单链表的随机存取,即不能通过直接找到链表中的某个节点。在数组中可以通过元素的位置(即下标),直接找到这个元素。而在链表中却不能这样做,必须从头开始遍历,直到找到要查找的元素。
基本操作
首先定义一个单向链表的顺序表结构。
public class SingleLinkedList <T> {
/**
* 链表的头指针
*/
private Node<T> head; 3
/**
* 链表的尾指针
*/
private Node<T> tail; 4
/**
* 链表的大小
*/
private int size = 0;
}
head指向链表的头节点,因此称为头指针。头指针指向链表的第一个节点,如果头指针为null,则说明链表是空的。tail指向链表的尾节点,因此称为尾指针。
当链表中没有任何元素时,也即链表为空,head 和 tail 都为空,如果只有一个元素时,head 和 tail都指向这个元素。
之所以要存储尾节点,是因为采用尾插法添加数据时,可以使时间复杂度降到 。
添加元素
链表中添加元素的方法有两种:头插法和尾插法。具体如下
头插法
头插法就是将新的元素添加到链表的头部。操作步骤如下:
- 将新节点的后继指针指向头节点
- 将头指针指向新节点
代码实现如下:
public void addFirst(T data) {
Node<T> node = new Node<>(data);
if (head == null) {
head = tail = node;
} else {
node.setNext(head); 1
head = node; 2
}
size++;
}
- 当头节点为空时,将头尾指针都指向新节点。
- 当头节点不为空时,先将新节点的指针指向头节点,再将头指针指向新节点。
注意节点 A, 在执行 node.setNext(head) 时,head 指向的是 A,因此 node.setNext(head) 相当于是将新节点指向了 A。在理解时,要注意图上的序号。
头插法操作的时间复杂度是 。
尾插法
尾插法就是将新的元素添加到链表的尾部。代码实现如下:
public void addLast(T data) {
Node<T> node = new Node<>(data);
if (head == null) {
head = tail = node;
} else {
tail.setNext(node); 1
tail = node; 2
}
size++;
}
tail.setNext(node) 在执行时,tail 指向的是节点 T,也就是当前的尾节点。因此 tail.setNext(node) 相当于是将节点 T 的 next 指针指向了新的节点。
由于我们存储了尾指针,因此尾插法的时间复杂度是 ,如果没有存储尾指针,要获取到尾节点,就需要遍历这个链表,其时间复杂度就是 。
插入元素
即在指定的索引位置插入元素。如果指定的索引位置超过链表长度则抛出异常,如果指定的位置小于 0 ,同样抛出异常。
代码如下:
public void add(int index, T data) {
if (index < 0 || index > size()) {
throw new IllegalArgumentException("index out of range");
}
if (index == 0) {
addFirst(data);
return;
} else if (index == size()) {
addLast(data);
return;
}
// 找到插入的位置的前一个节点
Node<T> pre = getNode(index - 1); 1
Node<T> node = new Node<>(data);
node.setNext(pre.getNext()); 2
pre.setNext(node); 3
size++;
}
private Node<T> getNode(int index) {
if (index < 0 || index > (size() - 1)) {
throw new IllegalArgumentException("index out of range");
}
Node<T> node = head;
for (int i = 0; i < index; i++) {
node = node.getNext();
}
return node;
}
- 节点上的数字代表节点的索引。
- 向索引位置 3 插入元素的含义是,新节点插入到 3 的位置,原索引位置为 3 及其之后的节点后移。
由于需要通过索引查找元素,这会导致需要遍历链表,因此最坏情况下算法的时间复杂度是
查找元素
指定索引查��找
在插入元素部分已经实现过按照指定索引查找节点的功能。只需要提供一个方法返回节点数据即可。如下:
private Node<T> getNode(int index) {
if (index < 0 || index > (size() - 1)) {
throw new IllegalArgumentException("index out of range");
}
Node<T> node = head;
for (int i = 0; i < index; i++) {
node = node.getNext();
}
return node;
}
public T get(int index) {
Node<T> node = getNode(index);
return node.getData();
}
也可以直接返回节点 Node<T>,但是考虑到实际应用中,我们一般不关注于顺序表的底层结构(数组实现或链表实现),而是通过其上层 API 来操作顺序表。因此我们只关心顺序表中的数据,而不关心其存储结构。
返回节点实际上是返回了一个链表的子链,其风险是可以在链表(SingleLinkedList)外部对这个子链进行操作,如插入节点、删除节点。而这些操作可以不通过其 API 来实现。
顺序表的概念后文中再将,现在可以将其理解为就是 Java 中的 List。而我们现在实现的是一个底层数据结构为单向链表的顺序表。类似于 Java 中的 LinkedList。
判断元素是否在链表中
从头开始遍历节点,并判断节点内的数据与要判断的数据是否一致。如果链表中存在节点与所查数据一致则返回 true,否则返回 false。
private boolean has(T data) {
Node<T> node = head;
while (node != null) {
if (node.getData().equals(data)) {
return true;
}
node = node.getNext();
}
return false;
}
删除元素
由于单向链表的单向性,删除头部节点的时间复杂度是 ,而删除尾部节点的时间复杂度是 。因为虽然保存了尾指针,但是无法从尾节点找到上一个节点,必须从头开始遍历。
删除头部元素
删除头部元素只需要将头指针指向链表头部元素的下一个节点即可。实现代码如下:
public Node<T> removeFirst() {
if (head == null) {
throw new IllegalArgumentException("list is empty");
}
Node<T> node = head;
head = head.getNext();
node.setNext(null);
size--;
if (size == 0) {
tail = null;
}
return node;
}
删除头部节点不需要遍历链表,因此算法的复杂度是 。
这里之所以将删除头部节点,实际上是在为后续的队列数据结构铺路。我们知道队列是先进先出(FIFO)的,先添加到队列中的元素先出队。我们从头部删除就可以视为将先添加的元素出队。
这里要注意这段代码:
if (size == 0) {
tail = null;
}
当链表中只有一个元素时,我们执行 removeFirst 方法,会将 head 指针置为 null,但是没有将尾指针置空。在所有的判空操作中,我们只判断了 head 指针,因此逻辑上没有什么问题。再进行添加和删除依然能得到正确的结果。
这里只会存在一个 GC 问题,由于 tail 指向了这个节点的引用,因此在新的节点被添加进来之前这个节点不会被回收。或者随着链表一起被回收。请注意这个细节。下面这种写法也是可以的。
public Node<T> removeFirst() {
if (head == null) {
throw new IllegalArgumentException("list is empty");
}
Node<T> node = head;
size--;
if (size == 0) {
head = null;
tail = null;
} else {
head = head.getNext();
node.setNext(null);
}
return node;
}
删除尾部元素
我们无法从尾部指针获取到尾部元素的上一个元素,因此只能通过遍历链表的方式来获取。因此删除尾部元素需要经过一次链表的遍历。
public Node<T> removeLast() {
if (head == null) {
throw new IllegalArgumentException("list is empty");
}
Node<T> node = tail;
tail = getNode(size - 2); 1
tail.setNext(null); 2
size--;
if (size == 0) {
head = null;
}
return node;
}
tail.setNext(null) 在这个方法尤为重要,切不可遗漏。否则虽然将尾指针前移了,但是链表并没有断开,在遍历时可能会取到已删除的节点。
由于需要遍历链表,因此其算法的时间复杂度是 ,在后面讲到双向链表的时候,会了解到这个算法的时间复杂度会变为 。因为双向链表无需遍历链表,可以直接通过尾指针获取到上一个节点。
在后续的章节中我们会了解到栈是一种后进先出的结构。因此从尾部删除元素其实就是栈的链表实现的一部分。而从上面介绍的算法效率来看,使用单向链表来实现栈结构,并不是一种很好的方式。因此一般我们会采用数组或双向链表来实现栈结构。
删除指定位置的元素
即通过给定的索引来删除元素。首先要判断索引的合法性,其次要删除的元素是不是在首尾节点。如果在首尾节点直接调用删除头部元素和删除尾部元素的方法来处理。
public Node<T> remove(int index) {
if (index < 0 || index > size()) {
throw new IllegalArgumentException("index out of range");
}
if (index == 0) {
return removeFirst();
}
if (index == size() - 1) {
return removeLast();
}
Node<T> pre = getNode(index - 1); 1
Node<T> node = pre.getNext(); 2
pre.setNext(node.getNext()); 3
node.setNext(null);
size--;
return node;
}
由于需要遍历链表,因此算法的时间复杂度为
遍历元素
上面已经多次使用过链表的直接遍历,其实就是不停的获取下一个节点,如果下一个节点为 null 则链表结束。下面我们实现另外两种,一种是迭代器,一种是流。流是基于迭代器的。
迭代器
- 实现迭代接口:
java.lang.Iterable - 实现方法:
Iterator<T> iterator()
迭代接口的代�码如下(限于篇幅,删除了注释部分,如果想看注释,可以从 JDK 源码中查看):
public interface Iterable<T> {
Iterator<T> iterator();
default void forEach(Consumer<? super T> action) {
Objects.requireNonNull(action);
for (T t : this) {
action.accept(t);
}
}
default Spliterator<T> spliterator() {
return Spliterators.spliteratorUnknownSize(iterator(), 0);
}
}
这里之所以列出 java.lang.Iterable 的源码,是因为后面在实现流的时候会用到 spliterator() 方法。
实现方法 Iterator<T> iterator() 的代码如下:
public Iterator<T> iterator() {
return new Iterator<>() {
private Node<T> node = head;
@Override
public boolean hasNext() {
return node != null;
}
@Override
public T next() {
if (node == null) {
throw new NoSuchElementException("链表为空或已遍历至链表尾部");
}
Node<T> data = node;
node = node.getNext();
return data.getData();
}
};
}
迭代器的使用
实现了迭代器接口后我们就可以使��用 for-in 这种语法来遍历链表中的元素了。
public static void main(String[] args) {
SingleLinkedList<Integer> singleLinkedList = new SingleLinkedList();
singleLinkedList.addLast(1);
singleLinkedList.addLast(2);
singleLinkedList.addLast(3);
// 使用迭代器遍历链表
Iterator<Integer> iterator = singleLinkedList.iterator();
while (iterator.hasNext()) {
System.out.println(iterator.next());
}
// 使用 for-in 语法遍历元素,与上面的迭代器遍历,效果一样。
for (Integer i : singleLinkedList) {
System.out.println(i);
}
}
流 (Stream)
流的实现方式非常简单,只需要将迭代器转为流即可。
public Stream<T> stream() {
return StreamSupport.stream(spliterator(), false);
}
// 并行模式流
public Stream<T> parallelStream() {
return StreamSupport.stream(spliterator(), true);
}
这里的 spliterator() 就是迭代器中的 spliterator() 方法。
总结
单向链表相关操作的算法的时间复杂度如下:
| 算法 | 时间复杂度 |
|---|---|
| 插入元素(头插法) | |
| 插入元素(尾插法) | |
| 插入元素(按索引) | |
| 查找元素 | |
| 删除头部元素 | |
| 删除尾部元素 | |
| 删除指定位置元素 |
单向链表的数据获取至少需要经过两次访存。因此比数组效率要低。






